问题

众所周知，系统的冲激响应和频率响应是一对傅里叶变换对。也就是说，只需要将系统的冲激响应进行傅里叶变换，然后再经过一些处理，即可得到系统的幅频响应曲线和相频响应曲线。在 MATLAB 中，我们可以使用 fft 函数来进行快速傅里叶变换，但也可以使用 freqz 函数来直接求解数字系统的频率响应，按照上面的分析，这俩应该做的是一件事情，可是，它们的结果好像差距有点大？

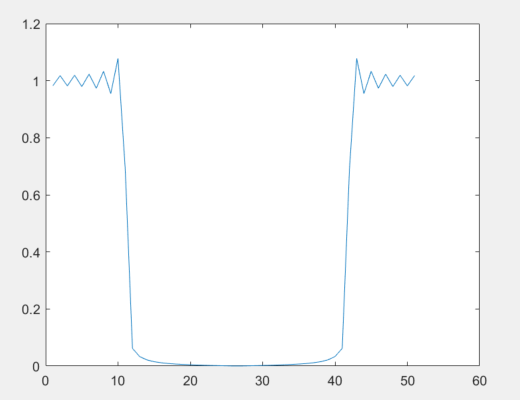
先试一下 fft 。

b = 0.4*sinc(0.4*(-25:25));
plot(abs(fft(b)));

通过 fft 得到的幅频响应曲线，结果是这样的：

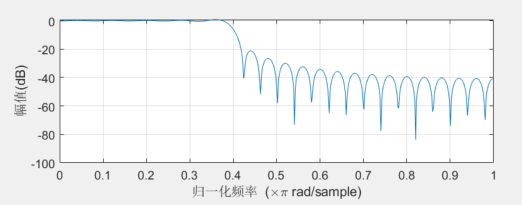
再试一下 freqz 。

b = 0.4*sinc(0.4*(-25:25));
freqz(b);

通过 freqz 得到的幅频响应曲线，结果是这样的：

这差的也太大了吧？

那么，为什么？

调查一下

这个问题得从多角度进行分析。

首先，FFT 本质上是 DFT 的优化，而 DFT 在频域上是离散的。试想：数字滤波器虽然是数字的，但是它的频率响应会是离散的吗？显然不是。
因此，想要从单位冲激响应画出数字系统的频率响应，我们需要的是 DTFT 而不是 DFT ，关于这俩的转换关系， 这篇文章 讲的非常通俗易懂。

其次，对实序列进行 FFT ，其结果有一半是共轭的，可以参照 这篇文章 当中的证明，因此其得到的幅频响应必然是对称的（上面的第一张图）。

所以，freqz 到底做了些什么呢？
首先，它会使用更高点数的 fft 来逼近 DTFT （默认是 500 点）。其次，它会自动帮你砍掉变换结果中的共轭部分。另外，还有一些细节处理，比如对数坐标。

尝试自己用 fft 实现一下？

b = 0.4 * sinc(0.4 * (-25 : 25));
res = abs(fft(b, 500));
semilogy(res(1 : length(res) / 2));

这下够像了吧？