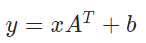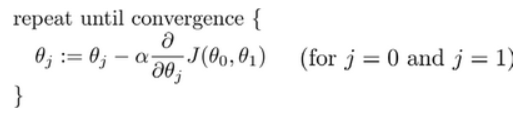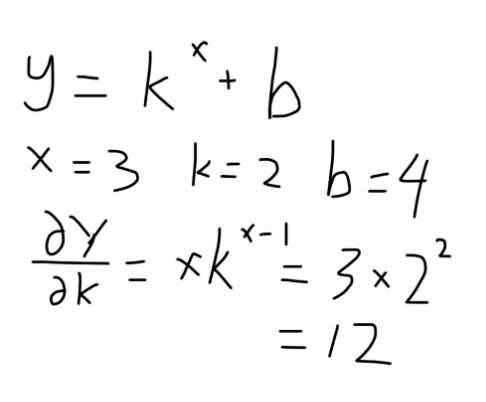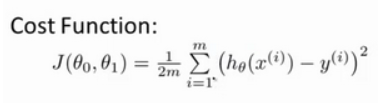前言
正文

import
数据
定义网络1 ~~（还是应该叫模型？模块？）~~
变量

它到底是啥？
额外参数和方法有啥？
它是如何工作的？

定义网络2
损失函数和优化器
开始训练
收尾工作

前言

嗯，ML这个东西，断断续续看了很久才在数学上勉强入门，但是一拿起框架，这都是什么JB？求导去哪儿了？梯度下降又在哪儿？数值是怎么传递的？这都是什么鬼？？

今天，抽出了一些时间，拨开了重重迷雾，算是勉强入门了Pytorch

当然，Python我也不会呐，那就再同时学学PY吧（笑

正文

首先奉上东拼西凑，成功跑通的代码

#!python

import torch
from torch import nn, optim
from torch.autograd import Variable
import numpy as np
import matplotlib.pyplot as plt
from torch.nn.parameter import Parameter
 
x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],
                    [9.779], [6.182], [7.59], [2.167], [7.042],
                    [10.791], [5.313], [7.997], [3.1]], dtype=np.float32)
 
y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],
                    [3.366], [2.596], [2.53], [1.221], [2.827],
                    [3.465], [1.65], [2.904], [1.3]], dtype=np.float32)
                    

x_train = torch.from_numpy(x_train)
 
y_train = torch.from_numpy(y_train)

class LinearRegression(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(1, 1)
 
    def forward(self, x):
        out = self.linear(x)
        return out


model = LinearRegression()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-2)

num_epochs = 10000

inputs = Variable(x_train)
target = Variable(y_train)
for epoch in range(num_epochs):
    out = model(inputs)
    loss = criterion(out, target)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
 
    if (epoch+1) % 20 == 0:
        print("Epoch[%d/%d], loss: {:%.6f}"%(epoch+1, num_epochs, loss.data))

model.eval()
predict = model(x_train)
predict = predict.data.numpy()
plt.plot(x_train.numpy(), y_train.numpy(), 'ro', label='Original data')
plt.plot(x_train.numpy(), predict, label='Fitting Line')
plt.legend() 
plt.show()

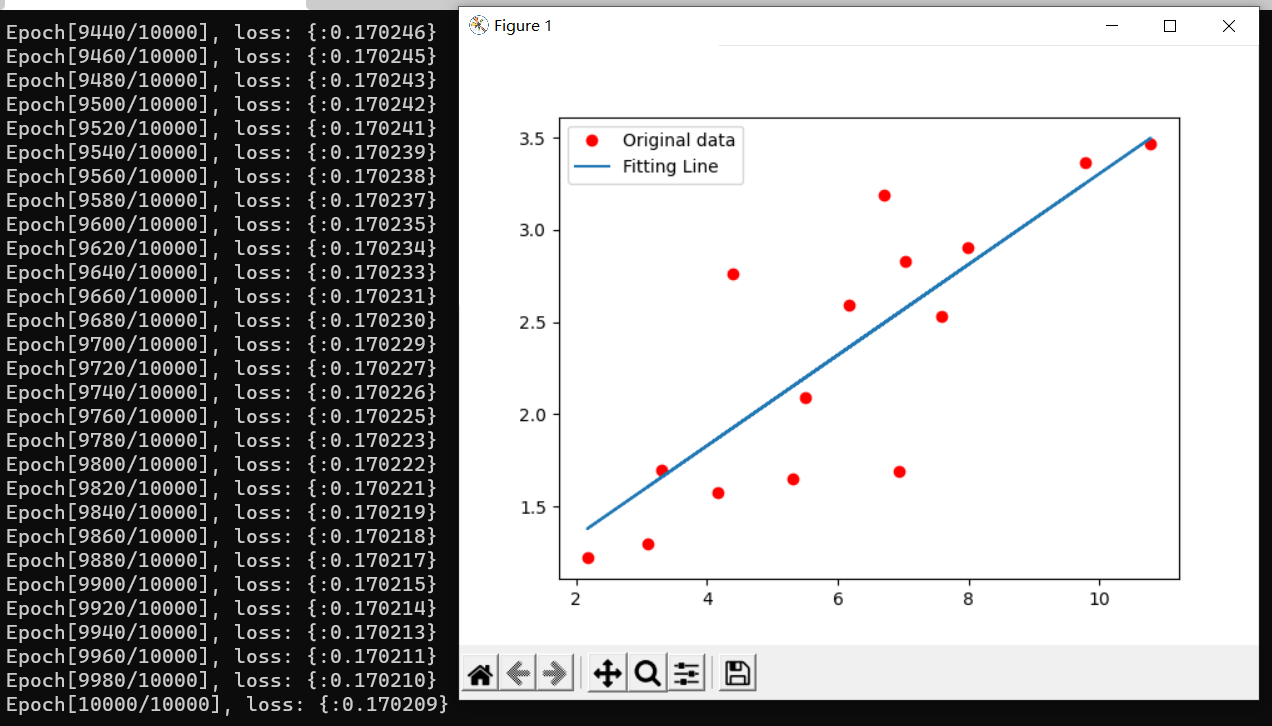
运行效果

接下来逐行细细道来，大概的梳理一下Pytorch是怎么运行的

import

#!python

import torch
from torch import nn, optim
from torch.autograd import Variable
import numpy as np
import matplotlib.pyplot as plt

啊，这没什么必要解释了吧，第一行是给cygwin下的bash的，剩下的就是导包，至于Python导包的语法，我在这里曾经稍微记录了一下

数据

x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],
                    [9.779], [6.182], [7.59], [2.167], [7.042],
                    [10.791], [5.313], [7.997], [3.1]], dtype=np.float32)
 
y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],
                    [3.366], [2.596], [2.53], [1.221], [2.827],
                    [3.465], [1.65], [2.904], [1.3]], dtype=np.float32)
                    

x_train = torch.from_numpy(x_train)
 
y_train = torch.from_numpy(y_train)

嗯，这里挺有趣的，是Pytorch和numpy这个著名的数值计算库相互配合，先使用numpy创建向量组，然后转为训练用的张量组
这组张量是长这个样子的

$ ./lr.py
tensor([[ 3.3000],
        [ 4.4000],
        [ 5.5000],
        [ 6.7100],
        [ 6.9300],
        [ 4.1680],
        [ 9.7790],
        [ 6.1820],
        [ 7.5900],
        [ 2.1670],
        [ 7.0420],
        [10.7910],
        [ 5.3130],
        [ 7.9970],
        [ 3.1000]])

（张量，就当成n维数组吧？一种作为神经网络输入输出的特殊数组？一维张量是向量，二维张量是矩阵，三维是个体？）
~~（其实也可以用python自带的array创建张量的，这里用了numpy我猜是信仰问题）~~

这里，每一行表示一组数据，因为一组数据只有一个输入（x值）（因为这是最简单的线性回归模型），因此一行只有一个数据。在稍微复杂一点的模型下，一组数据可以有多个输入（类似多元函数）

$ ./lr.py
tensor([[ 3.3000,  1.0000],
        [ 4.4000,  1.0000],
        [ 5.5000,  1.0000],
        [ 6.7100,  1.0000],
        [ 6.9300,  1.0000],
        [ 4.1680,  1.0000],
        [ 9.7790,  1.0000],
        [ 6.1820,  1.0000],
        [ 7.5900,  1.0000],
        [ 2.1670,  1.0000],
        [ 7.0420,  1.0000],
        [10.7910,  1.0000],
        [ 5.3130,  1.0000],
        [ 7.9970,  1.0000],
        [ 3.1000,  1.0000]])

不知你注意到了没有，这里有点迷惑
np.array([[3.3],....[x.x]], dtype= ...)
为啥要在数组的元素外面再套一层壳呢？

哈，其实道理很简单，这整个东西作为函数的第一个参数呐，因为它不支持把一堆元素作为一个一个参数传进去...传进去的东西要求是一个能够返回Array的对象（即对象继承def __array__ (self)接口？），那，在外面套一层壳最简单了。。
（当然，这只是最简单的理解方式）

更深入一点理解，
一个张量如果外面没有[，那就是一个数
如果只有一层[，那就是一个向量
如果有两层[[，那就是一个矩阵
如果有三层[[[，那就是一个体

测试方法很简单，矩阵相乘（torch.mm）方法仅仅只适用于二维张量，否则会报错RuntimeError: self must be a matrix

也就是说，我们的测试数据，都是以矩阵的形式传入的

那能不能像这样，把内层的壳去掉呢？

x_train = np.array([3.3, 4.4, 5.5, 6.71, 6.93, 4.168,
                    9.779, 6.182, 7.59, 2.167, 7.042,
                    10.791, 5.313, 7.997, 3.1], dtype=np.float32)

也是不行的，在执行线性回归的基本操作时会报错

RuntimeError: mat1 and mat2 shapes cannot be multiplied (1x15 and 1x1)
我们之前传入的是一个15x1的矩阵，与一个1x1的矩阵相乘，得到一个15x1的结果（线性代数基操）
而现在，这个具有15个元素的向量被当成了一个1x15的矩阵，一乘就炸了

嗯，所以数学和写代码还是有些不一样，数学上，我们似乎不太区分向量和只有一行/一列的矩阵

定义网络1 （还是应该叫模型？模块？）

class LinearRegression(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(1, 1)
 
    def forward(self, x):
        out = self.linear(x)
        return out

先来学Python，class LinearRegression(nn.Module):表示这个类继承于nn.Module，而nn.Module是所有模型与神经网络的基类
然后，在Python里，类中的每一个函数的第一个参数都必须是指向自身对象的指针（一般都取名为self，java写多了取名成this也行（笑）

来看看一个网络能做的基操是啥
很简单，那就是这样

foo = LinearRegression()
#创建对象，py不需要new，因此总是屑屑的和方法搞混

foo(inputs)
#嗯？这是对象还是方法？
#这是py的特性，只需要在对象中定义def __call__ (self, .....)
#就可以把一个对象像方法一样调用了，是不是很离谱

至于那个inputs，可以是一个张量，也可以是一个变量（带反向传播功能的张量）(下面再说)
这个张量中包含n行，每一行表示一个输入
模型返回的结果也是一个n行的张量，每一行代表一个模型的输出
给输出，出输出，这就是一个网络呐

接下来看看这个网络的类里干了啥，首先是构造函数

def __init__(self):
    super().__init__()
    self.linear = nn.Linear(1, 1)

super().__init__()调用父类的构造函数，不看了，又懒又菜

self.linear = nn.Linear(1, 1)，这才是关键，或者可以说，是这个网络的实际内容（因为没别的东西了）
首先，它给自己这个对象加了个linear属性（没错，py就是像js一样，可以随手加属性，是不是很离谱？），指向一个nn.Linear对象，其构造参数为(1,1)

nn.Linear是一个封装好的，专门用于线性回归的nn.Module（没错，我们这个类继承的也是nn.Module，这是一个套娃行为），构造参数(1,1)代表，一维输入，一维输出（标准的 y = kx + b），其实它还可以有第三个布尔型参数，代表是否要有b，默认是True，如果指定为False就是强制过原点了。。。

那么，nn.Linear这个网络里面装着什么呢？

嗯，很显然里面有两个东西，一个是k，一个是b，它们不一定是一个数，也可以是一个向量甚至是矩阵（因为现在讨论的是最简单的情况）
当然，还装着这个网络是如何执行运算的（下面再说）

我们可以在训练完之后打印一下这个linear里面装着的参数

model = LinearRegression()
............
....训练....
............
print(model.linear.weight)#这是k
print(model.linear.bias)#这是b

结果

Parameter containing:
tensor([[0.3645]], requires_grad=True)
Parameter containing:
tensor([0.0204], requires_grad=True)

里面装着我们这个简单线性函数解出来的k和b的值，还有一个奇怪的东西？别急，因为这不是一个简单的张量，它是一个变量

变量

Variable，是Pytorch自动求导机制和反向传播机制的关键一环
在继续前进之前，我们必须先搞清楚变量是什么，它存储着什么，有什么作用，是怎么工作的，这对于理解Pytorch的工作流程极为重要

~~当然，先记住我们上面讲到了一个网络的构造函数里的套娃网络里的参数，关键的前向传播都还没讲呢~~
~~这里可能有点长，先把刚刚讲到哪儿记好了~~

它到底是啥？

我也不知道，暂且可以把它理解为带有额外参数的张量（这里迷惑的点是，打印变量的type，居然是简单的tensor（张量））

额外参数和方法有啥？

只讲几个接下来可能会牵扯到的

布尔型 requires_grad
梯度（大概是浮点型） grad
方法的引用 grad_fn
反向传播方法 backward()

不过其实这些东西一点也不额外，普通的张量也有这些属性，但是只有在Variable()之后才能主动使用它们？

它是如何工作的？

只要把这里弄懂，理解接下来的模型训练过程几乎就没有任何问题了
将Pytorch框架与数学理论相结合也没有任何问题了

众所周知，对于线性回归的梯度下降法，我们最终需要的是求代价函数关于参数的偏导数

这里问题的关键，就在于，求偏导这个过程在Pytorch中是如何实现的

众又所周知，偏导和梯度是差不多的概念（数学上，梯度就是把对各个变量的偏导放在一起组成一个向量）
因此，在Pytorch中，某个东西对a的偏导数就可以表示为a.grad (a是一个变量Variable)，而这个东西是什么（谁对a的偏导数），则取决于由谁开始反向传播backward()

举个例子

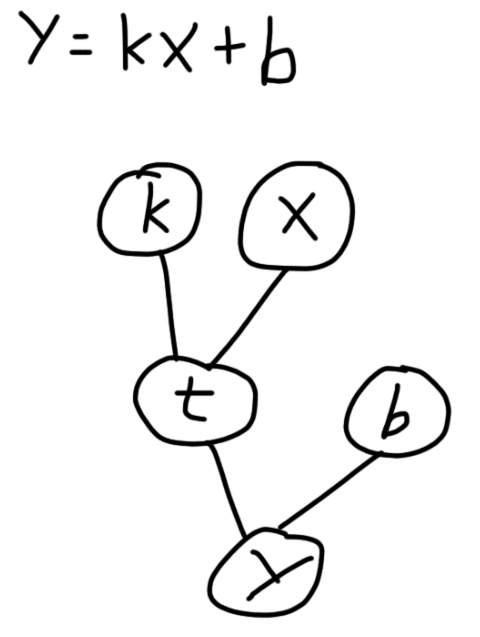
这是用计算图的形式来表示一个一元函数，变量k与x相乘形成临时中间变量t，然后t再与b相加得到y

这里的变量都指Variable

如果我想要求y对x的偏导（在x=x时的值），那么，只需要将x的requires_grad设置为True，然后对y执行backward()，那么y对x的偏导就会沿着路径一路求导（用哪个函数求导可以通过.grad_fn属性查看），一路传播过来。一路上，会根据计算图上各节点的连接方式不同（比如加减乘除，甚至各种更加复杂的cost function）进行分步求导，因此，从反向传播的起点到终点之间的所有节点（变量），其requires_grad都会被设置为True，并将中间偏导值存储在其中。对于本例来说，求导路径如下图所示

所以路径上牵扯到的节点y和t的requires_grad都会被自动设置为True

到这里，一切的关键，变量与求导，完成了，可以继续了

接一个上文，在上面我们可以看到，linear对象中的weight和bias的requires_grad都为True，这是自动帮你设置的，为啥呢？因为这两个东西就是我们最终要求的啊，我们要对它们求导啊。它们两个，就是反向传播的终点

最后再给个demo？

#!python

import torch
from torch.autograd import Variable
 
x = Variable(torch.tensor(3.0))
k = Variable(torch.tensor(2.0), requires_grad = True)
b = Variable(torch.tensor(4.0))
y = k ** x + b

y.backward()
print(k.grad)

它干的事情，是求y对k的偏导在k=2，x=3处的取值

手算一下

电脑算一下

$ ./test.py
tensor(12.)

嗯，符合的很好

定义网络2

我们继续回到这个东西

class LinearRegression(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(1, 1)
 
    def forward(self, x):
        out = self.linear(x)
        return out

之前，讲到了我们定义了一个网络，里面有个linear，这个linear也是一个网络（套娃行为）
那么，接下来，就来看看网络是如何工作的

主要就是这一块

def forward(self, x):
    out = self.linear(x)
    return out

前向传播方法
还记得上面提到的网络是如何使用的吗？给一组输入，提供一组输出，而输入到输出之间的关系，就是由前向传播方法决定
在此处，我们直接调用了内部的网络，并返回其输出值作为外部网络的输出值，而这个过程则会调用Linear这个网络的前向传播方法，并在其中对输入数据进行处理，得到输出

引用一句别人的话
“对于一个神经网络模型来说，确定这个模型有哪些层以及这些层之间的数据如何流动，那这个模型就确定了。所以模型的__init__方法声明模型有哪些类，模型的forward方法规定数据如何在层之间流动。”

那么问题来了，能不能这样呢？

class LinearRegression():
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(1, 1)
 
    def forward(self, x):
        out = self.linear(x)
        return out

我不继承nn.Module，仅仅只是定义层与前向传播方法

emmm，我觉得直接拿来用是没有任何问题的，反向传播和求梯度也不会产生什么问题，问题只会发生在优化器的使用上（其实是在盲猜），下面再说

损失函数和优化器

继续向下分析代码

model = LinearRegression()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-2)

此处，我们为我们自己定义的网络（模型）创建了一个对象
对于这个对象，我们可以直接使用model(inputs)来获得输出值

然后，我们定义了一个损失函数的对象，它是什么，又和标准的梯度下降有什么关系呢？

不如直接来看看MSELoss的定义吧

解释一下：在默认情况下，就是各项求平方和之后求平均值

嗯？这不就是线性回归，梯度下降中的平方损失函数么...

它们的差异也许只有为了求导方便多除了一个2，然而这无关痛痒....

也就是说，MSELoss，就是我们所使用的平方损失函数

它该如何使用呢？别急，接下来的代码分析里就会遇到

那optimizer = optim.SGD(model.parameters(), lr=1e-2)呢？

课上我们使用的是梯度下降

而这里的SGD，根据文档来看，就是指随机梯度下降

传入的第一个参数，是我们所使用的网络的参数，第二个则是学习率

嗯？是不是有点好奇。我们的网络是一个套娃网络，一个外壳网络套了一个内部的真正线性回归网络，那么model.parameters()究竟能得到什么？？

很有意思，model.parameters()竟能够返回我们层层套娃的所有网络的参数！
它是怎么做到的呢？
其实秘密就在这里
self.linear = nn.Linear(1, 1)
别觉得linear有啥问题，这个名字取啥都行，有问题的是.这个东西
Python为类提供了别致的魔法方法__setattr__()，能够轻松的拦截这种给对象加属性的操作，而nn.Module正是继承了这一接口，将赋值作为属性的子网络，通通放入了一个子网络列表中，参数就能随便遍历啦

诶，还有个问题，那它又是怎么知道一个网络有什么参数的呢？那些参数也好像是非常普通的属性诶。。

Pytorch提供了Parameter(tensor)这个类，能够将一个张量转为一个“网络参数”，它和变量其实并没有什么区别（不过它的requires_grad默认就为True），而Parameter的特点就在于，我们把它当作属性赋值给一个网络时，就会像上面的子网络一样，被魔法方法拦截，并增加到参数列表中。
比如Linear网络的b参数，就是这样被添加进去的self.bias = Parameter(torch.Tensor(out_features))

最后，优化器和损失函数是如何工作的呢？接着往下看

开始训练

num_epochs = 10000

inputs = Variable(x_train)
target = Variable(y_train)
for epoch in range(num_epochs):
    out = model(inputs)
    loss = criterion(out, target)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
 
    if (epoch+1) % 20 == 0:
        print("Epoch[%d/%d], loss: {:%.6f}"%(epoch+1, num_epochs, loss.data))

num_epochs = 10000，定义了要训练多少次
inputs = Variable(x_train)和target = Variable(y_train)则是把输入和输出由单纯的张量转为了变量，不过我试了一下，不转也是没有任何问题的。张量和变量并没有进行什么明显的区分，普通张量也具有grad、requires_grad之类的属性，也许变量存在的意义仅限于作为求梯度的对象吧.....嗯，不影响大局，以后有机会再研究吧

当然，还有另一种理解，x_train和y_train都没有在求导路径上，因此即使它们没有保存梯度的地方也没什么关系（不过，如果在求导路径上，它们作为结果，自然就是变量了....）

无论怎么理解，对功能都没有任何影响，那就继续扒
out = model(inputs)，将数据作为矩阵输入到网络中，一行是一组数据，得到的out是输出，一行为一组输出
loss = criterion(out, target)，使用上面定义的代价函数对象，将包含网络算出的结果和正确结果的矩阵传入，一行为一组数据，得到一个0维张量（变量）作为输出（0维张量说白了就是一个数嘛）

然后
optimizer.zero_grad()
这是将我们的网络中的变量的梯度都设置为0，原因是Pytorch的梯度是累加的，不清零会出问题
你可能会好奇，optimizer对象是怎么影响模型的梯度的呢？很简单，我们之前把它传进去了呐optimizer = optim.SGD(model.parameters(), lr=1e-2)

继续
loss.backward()，上面所说的反向传播
optimizer.step()，根据上面反向传播，传给参数的梯度，按照优化器的规则（此处就是梯度下降），调整参数内容，改进模型

好了，到这里，损失函数和优化器的基本用法，大概也都知道了吧？

还有一个关键问题，从数学的角度看，这次训练，干了什么？
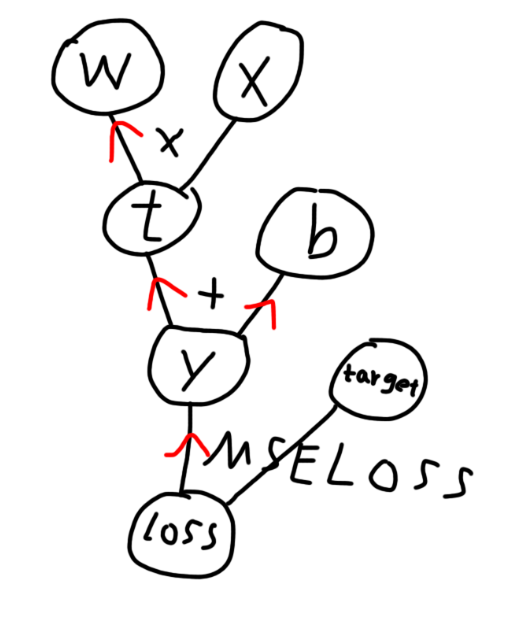
画了张计算图

其中MSELoss可以当成和加减乘除一样的玩意儿，也有对应的直接求导方法，不用操心啦
最终梯度会被传给我们的目标w（k）和b，然后由优化器进行梯度下降与优化

我们的x_train对应x，y_train对应target，out对应y，红色是梯度传播的方向
这也就印证了我上面的，x_train和y_train都不在求导路径上

收尾工作

if (epoch+1) % 20 == 0:
    print("Epoch[%d/%d], loss: {:%.6f}"%(epoch+1, num_epochs, loss.data))

打印训练情况

model.eval()
将模型设置为评估状态（对我们这个网络似乎没什么用..我们这个网络不会自己更新参数）

然后，打印图表，不解释了

predict = model(x_train)
predict = predict.data.numpy()
plt.plot(x_train.numpy(), y_train.numpy(), 'ro', label='Original data')
plt.plot(x_train.numpy(), predict, label='Fitting Line')
plt.legend() 
plt.show()

算了，还是解释一下吧，这里给的数据并不是直接基于网络里的参数绘制一条直线，而是将训练集的东西丢进模型得到结果，然后用结果（散点）拟合一条直线（怪起来了），如果我们指定参数"o"，强制其成为散点，那拟合的直线就看不到了（笑

结

内卷壬怎么能少了ML呢？

Pytorch的第一次——线性回归

前言

正文